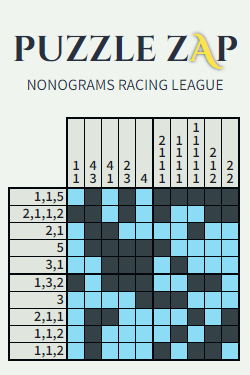
Puzzle Zap is a website for playing nonograms (logical puzzles), where users race against themselves and others to complete nonograms as fast as possible. If you aren't familiar with nonograms, the Puzzle Zap How To Play page explains what nonogram puzzles are and how to solve them. The recording below shows a Puzzle Zap nonogram being solved.
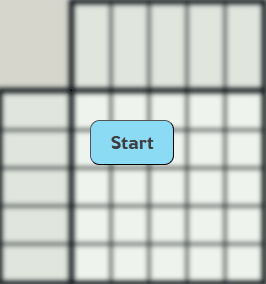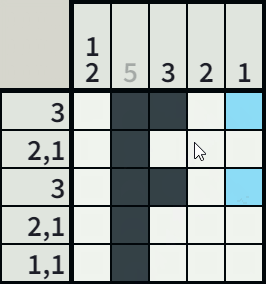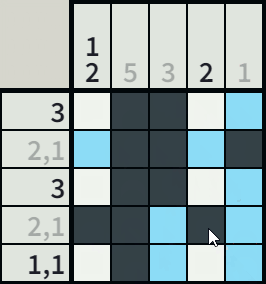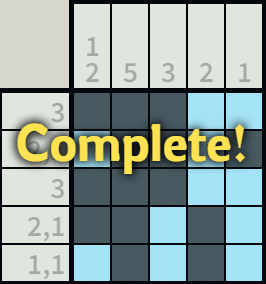
Puzzle Zap was launched in 2023 and continues to be developed with new features. Current features:
- Speed challenges on a range of grids (5x5, 10x10, 15x15, 20x20, 25x25, 30x30)
- Daily challenge (get once chance to play a 5x5, 10x10, and 15x15)
- High score boards for each grid with user progression charts and user replays

Project Challenge: Generate Difficult Nonograms
Solution: Build a Nonogram Solver
Generating uniquely solvable nonograms isn't a trivial challenge. Generating very difficult uniquely solvable nonograms is a slightly harder challenge still. I ended up taking the following approach:
- Generating a large number of grids by randomly filling in the grid cells as either filled or flagged.
- Calculating the hints for each grid.
- Process the hints with a nonogram solver to determine whether each grid is uniquely solvable and to classify the nonogram's difficulty.
- Select only the most difficult nonograms to put on Puzzle Zap for users to play.
All the steps are relatively easy except for step 3, so that's what the remainder of this section will discuss.
Initially, I checked all the publicly available Python nonogram solvers that I could find to see if they could be easily modified to suit my needs. However, nearly all the solvers I found were too slow to be viable for my approach (after all, solving nonograms is an NP-complete problem). And of the solvers that were less slow (but still probably too slow for my approach), I wasn't able to easily modify them to where I could classify grids based on difficulty.
So I ended up taking on challenge of building my own solver. Instead of using the common (computationally expensive) approach of calculating all possible permutations for each line (given the line's hints) to see what can be filled in, I decided to build my solver to solve nonograms the same way I manually solve nonograms. The specifics of how I manually solve a nonogram are laid out on the How To Play under the section "Line Solving Examples". I just put those rules into code to build my solver. While solving, the script counts the number of steps it takes to solve the nonogram. A higher number of required steps indicates that the nonogram is harder to solve.
Once I had my solver, I generated 1000 randomized grids of various sizes (5x5, 10x10, 15x15, 20x20, 25x25, 30x30) and processed them with my solver. Then I plotted the results on graphs to show me the solves steps versus filled square percent to determine the optimal filled percent range I should be using to generate the hardest grids.
This chart shows the distribution of 5x5 grids (note: 0 solve steps means the grid isn't solvable).
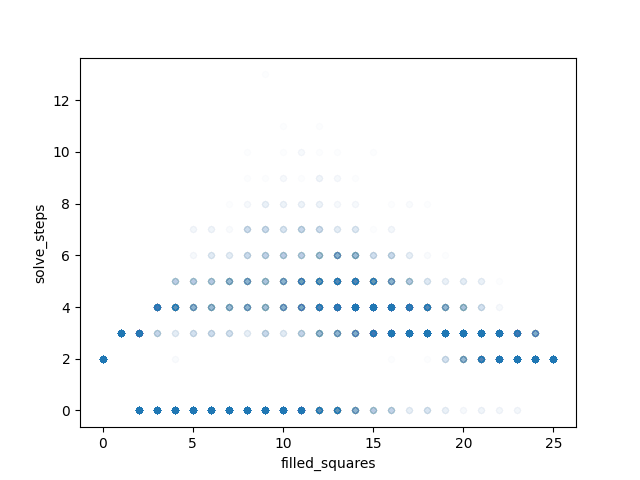
Using the graph above, I selected a filled square percent range to use. Then I let the script randomly generate and process 100,000 grids for each of the grids sizes I wanted to host on Puzzle Zap. All computations were done on my modest home PC. Below are the processing times for randomly generating and processing/categorizing the grids.
| Grid Size | Process Time | Average Grids Processed Per Second |
|---|---|---|
| 5x5 | ~1.5 minutes | 1176 |
| 10x10 | ~4.5 minutes | 357 |
| 15x15 | ~9 minutes | 183 |
| 20x20 | ~16 minutes | 105 |
| 25x25 | ~24 minutes | 69 |
| 30x30 | ~35 minutes | 48 |
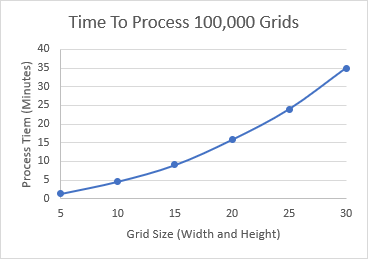
As you can see, the process times get significantly longer as the grids get bigger. In fact, it might be more informative to plot the x-axis as the total number of cells in a grid (width * height) instead of just by the grid size (width).
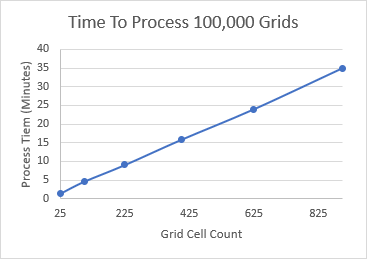
Ah, that's better... a nice linear relationship between the number of cells processed and process time. So if I want to generate larger rectangular grids in the future, I can estimate the processing time to decide whether it's worth it. Luckily, really large grids are also hard for humans to solve (and they don't display well on the screen), so I don't need to generate grids larger than 30x30 for now, since they would likely not be worth playing for most people.
Was all the effort worth it? I definitely think so. Being able to generate all the grids I want (with the exact parameters I care about and in relatively quick time) helps me create a better product. Outside the 5x5 grids (which don't have much variance in difficulty), the nonograms on Puzzle Zap are by far the hardest I've encountered.